[free]Gate 2022 CE solved paper with explantion pdf forenoon

Below the Gate 2022 Civil Engineering solved question paper(forenoon session ) which were held on 12-02-2022. The total number of questions are 65, 10 from aptitude and 55 from Civil Engineering. Question paper is cover in 7 pages and each page have 10 questions. Question on this page from 11 to 20.

Quick links :

10 questions of Aptitude 55 questions of Civil Engineering

Do you know ? You can check your knowledge by clicking any option with the help of in build practice mode without checking detail solution, while reading gate CE paper . With this know the level of your preparation and make a study plan for it.

Let’s start

Question 11.

Consider the following expression:
$z = sin (y + it) + cos(y - it)$
where $z, y \textrm{ and} \, t$ are variable, and $i = \sqrt {-1}$ is a complex number. The partial differential equation derived from the above expression is

\dfrac{d^2 \textrm{z}}{d \textrm{t}^2} + \dfrac{d^2 \textrm{z}} {d \textrm{y}^2 } = 0

\dfrac{d^2 \textrm{z}}{d \textrm{t}^2} - \dfrac{d^2 \textrm{z}} {d \textrm{y}^2 } = 0

\dfrac{d \textrm{z}}{d \textrm{t}} - i \dfrac{d \textrm{z}} {d \textrm{y} } = 0

\dfrac{d \textrm{z}}{d \textrm{t}} + i \dfrac{d \textrm{z}} {d \textrm{y} } = 0

Previously Asked in : Gate CE 2022 ||

Detailed Explanation

$z = sin (y + it) + cos(y - it)$

Differentiation w.r.t. $y$

$\dfrac{d z} {d \textrm{y}} = cos(y + it) - sin(y - it)$

Formula used : $\frac {d }{d \textrm{x}} sinx = cos x ; \; \frac{d }{d \textrm{x}} cosx = - sinx$

\dfrac {d^2z}{dy^2} = -sin(y + it) - cos(y -it)

${\color {red} \boxed {\color {black} {\dfrac{d^2 z} {dy^2} = -z}}}$ … 1

Differentiation w.r.t. $t$

$\dfrac {d z}{d t} = i cos (y + it) +i sin (y - it)$

$\dfrac {d^2 z} {dt^2} = + sin (y + it) + cos (y - it)$

${\color {red} \boxed {\color {black} {\dfrac{d^2 z} {dt^2} = z}}}$ … 2

Adding 1 and 2 equations, we get

\dfrac {d^2z} {dy^2} + \dfrac{d^2 z} {dt^2} = 0

Correct option is: $\dfrac{d^2 \textrm{z}}{d \textrm{t}^2} + \dfrac{d^2 \textrm{z}} {d \textrm{y}^2 } = 0$

Question 12.

For the equation
$\dfrac {d^3y} {dx^3} + x \left (\dfrac{dy} {dx} \right) ^{ 3/2} + x^2y = 0$
the correct description is

an ordinary differential equation of order 3 and degree 2

an ordinary differential equation of order 3 and degree 3

an ordinary differential equation of order 2 and degree 3

an ordinary differential equation of order 3 and degree 3/2

Previously Asked in : Gate CE 2022 ||

Detailed Explanation

Given equation,

$\dfrac {d^3y} {dx^3} + x \left (\dfrac{dy} {dx} \right) ^{ 3/2} + x^2y = 0$

Power of $\left ( \dfrac {dy}{dx} \right )$ is fractional, make it integer. Squaring on both sides, the equation will be,

\left ( \dfrac{d^3y}{dx^3} \right )^2 + x^2 \left ( \dfrac {dy } {dx} \right )^3 + \left ( x^2y \right)^2 = 0

So the highest order = 3 and degree of the highest order derivative = 2

Correct option is: an ordinary differential equation of order 3 and degree 2

Question 13.

The hoop stress at a point on the surface of a thin cylindrical pressure vessel is computed to be 30.0 MPa. The value of maximum shear stress at this point is

7.5 MPa

15.0 MPa

30.0 MPa

22.5 MPa

Previously Asked in : Gate CE 2022 ||

Detailed Explanation

Note : Both 7.5 MPa or 15.0 MPa are correct

Formula used :

Longitudinal stress: $\sigma _L = \dfrac {pd}{4t}$
Hoop stress : $\sigma _h = \dfrac {pd}{2t} \; \textrm{or} \; 2 \sigma_L$
$\tau_{max} = \dfrac {\sigma_h - \sigma_L} {2}$

Solution :

Case- 1 Maximum shear stress in plane

Given, $\sigma _h= \dfrac {pd}{2t} = 30 \,\textrm{MPa}$

From above formula, $\sigma_L = \dfrac {\sigma_h} {2} = \dfrac {30}{2} =15 \,\textrm{MPa}$

\tau_{max} = \dfrac {30 - 15} {2} ={\color {red}\boxed{\color{black}{ 7.5 \, \textrm{MPa}}}}

Case – 2 Absolute maximum shear stress

\tau_{max} = \dfrac {\sigma_h - 0}{2} = \dfrac{\frac {pd}{2t} -0}{2}

= \dfrac {1}{2} \times \dfrac {pd}{2t} = \dfrac {1}{2} \times 30 = {\color{red} \boxed{\color{black}{15 \,\textrm{MPa}}}}

So correct option is : 7.5 or 15 MPa

Question 14.

In the context of elastic theory of reinforced concrete, the modular ratio is defined as the ratio of

Young’s modulus of elasticity of reinforcement material to Young’s modulus of elasticity of concrete

Young’s modulus of elasticity of concrete to Young’s modulus of elasticity of reinforcement material.

shear modulus of reinforcement material to the shear modulus of concrete

Young’s modulus of elasticity of reinforcement material to the shear modulus of
concrete

Previously Asked in : Gate CE 2022 ||

Detailed Explanation

It is the question of working stress method (i.e elastic theory)

In RCC, modular ratio is the ratio between modulus of Elasticity of Steel and modulus of Elasticity of Concrete. It is donated by ‘m’ .

m $= \dfrac {\textrm{E}_s} {\textrm{E}_c} = \dfrac{280}{3\sigma_{cbc}}$ [as per IS 456 code] where as

E_s is the Young’s modulus of elasticity of steel
E_c is the Young’s modulus of elasticity of concrete
$\sigma_{cbc} \;$ is the permissible compressive stress in concrete due to bending (in N/mm² )

the correct option is: Young’s modulus of elasticity of reinforcement material to Young’s modulus of elasticity of concrete

Question 15.

Which of the following equations is correct for the pozzolanic reaction?

Ca(OH)_2 +

Reactive Super plasticiser

+ H_2O \to

C-S-H

Ca(OH)_2 +

Reactive Silicon dioxide

+ H_2O \to

C-S-H

Ca(OH)_2 +

Reactive Sulphates

+ H_2O \to

C-S-H

Ca(OH)_2 +

Reactive Sulphur

+ H_2O \to

C-S-H

Previously Asked in : Gate CE 2022 ||

Detailed Explanation

Pozzolanic materials have no cementing properties itself but have the property of combining with lime to produce stable lime pozzolana compound which has cementitious property.

Pozzolana is considered as siliceous and aluminous materials and when added in cement it have SiO₂Al₂O₃ form.

So, Pozzolanic reaction:

$Ca(0H)_2 +$ Reactive silica-di-oxide $+ H_2O \to$ C-S-H gel or tobermonite gel

Correct option is: $Ca(OH)_2 +$ Reactive Super plasticiser $+ H_2O \to$ C-S-H

Learn more : Previous year Gate papers of Civil Engineering with detailed solution

Learn more : GATE 2022 All branches Aptitude Questions with detailed Solution

Question 16.

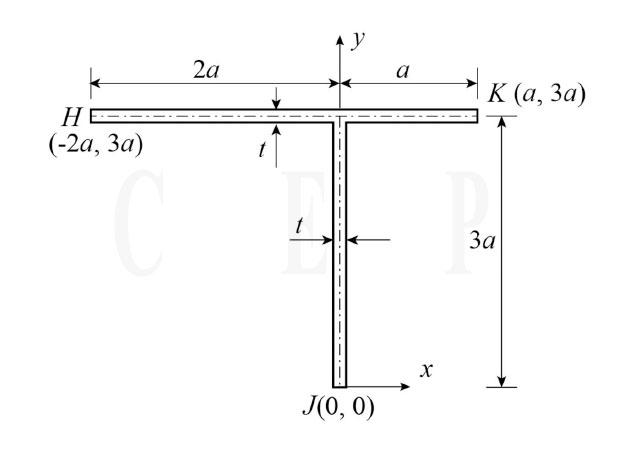
Consider the cross-section of a beam made up of thin uniform elements having thickness t (t << a) shown in the figure above. The (x,y) co-ordinates of the points along the center-line of the cross-section are given in the figure.
The co-ordinates of the shear center of this cross-section are:

x =0, y = 3a

x =2a, y = 2a

x =-a, y = 2a

x =-2a, y = a

Previously Asked in : Gate CE 2022 ||

Detailed Explanation

Shear center :

Shear center is a point on the cross section where the application of loads does not cause its twisting.

It is the point through which resultant of shearing force on the section passes, Shear center position is dependent on the cross- section of the beam

Few points should be remembered for finding the location of shear center on any cross section.

For symmetrical sections, the shear center and center gravity are the same and coincides with each other. shear center always lies on the axis of symmetry in this case.
For unsymmetrical section, the shear center lies on the axis where it has axis of symmetry.
For section consisting of two intersecting narrow rectangles always lies at the intersection of centrelines of two rectangles.

Examples :

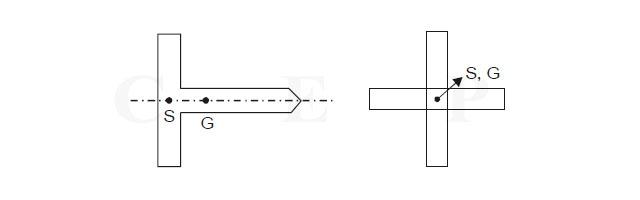
Notation: S= shear centre & G = centre of gravity

In this question, two rectangular have same thickness (t). So,

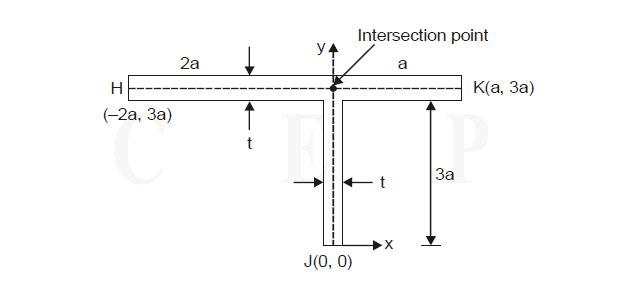
Coordinate of shear centre (0, 3a)

Correct option : x= 0 , y = 3a

Question 17.

Four different soils are classified as CH, ML, SP and SW, as per the Unified soil classification system.
Which one of the following options correctly represents their arrangement in the decreasing order of hydraulic conductivity?

SW, SP, ML, CH

CH, ML, SP. SW

SP, SW, CH, ML

ML, SP, CH, SW

Previously Asked in : Gate CE 2022 ||

Detailed Explanation

CH – clay with High liquid limit (> 50 %)
ML- silt with Low liquid limit (<50%)
SP – poorly graded sand with fines (<5%)
SW – well graded sand

AS per Allen Hazen’s formula , hydraulic conductivity / permeability (k) $= C \times {D_{10} }^2$

where C= constant $\left ( 100 \leq C \leq 150 \right )$ in cm & D₁₀ is effective diameter at which 10% of the grains are finer

$\therefore \; k \propto {D_{10} }^2$

Clay and silt are fine grained soils and Sand is coarse grained soil. More the dia more will be permeability. Well graded soil has better permeability than poorly graded. So Hydraulic conductivity order are as:

Sand > Silt > Clay

SW > SP > ML > CH

Correct option is : SW, SP, ML, CH

Question 18.

Let $\sigma'_v \textrm{and} \sigma'_h$ denote the effective vertical stress and effective horizontal stress, respectively.
Which one of the following conditions must be satisfied for a soil element to reach the failure state under Rankine’s passive earth pressure condition?

\sigma'_v < \sigma'_h

\sigma'_v > \sigma'_h

\sigma'_v = \sigma'_h

\sigma'_v + \sigma'_h = 0

Previously Asked in : Gate CE 2022 shift 1 ||

Detailed Explanation

Earth pressure is the lateral force exerted by the soil on any structure retaining that soil.

The ratio of the horizontal stress to the vertical stress is called the coefficient of earth pressure, i.e $K = \dfrac{\sigma_h}{\sigma_v}$

Types of earth pressure :

Active earth pressure
Passive earth pressure

Active earth pressure : When the wall is moving away from the soil, the soil mass expands, resulting in a decrease in earth pressure due to mobilization of shearing resistance. A portion of the backfill tends to break away from the rest of the soil mass and tends to move downward and outward relative to the wall. A stage is reached when the entire shearing resistance is mobilized and at this stage, the force acting on the wall is called active earth pressure.

It is given as ${\color{red} \boxed{\color{black}{\textrm{k}_a = \dfrac {\sigma_h}{\sigma_v} }}}$

where as K_a is always < 1 which means ${\color{red}\boxed {\color{black} { \sigma_h < \sigma_v}}}$

Passive earth pressure ( Kp ) : when the wall is pushed towards the backfill and the soil is compressed. Due to this, shearing resistance builds up in the direction of the wall.The earth pressure gradually increases and reaches a value where backfill cannot withstand and slip surface is formed. the force acting on the wall at this stage is called passive earth pressure.

Passive earth pressure is given as :

${\color{red} \boxed{\color{black}{\textrm{k}_p = \dfrac {\sigma_h}{\sigma_v} }}}$

where as K_p is always > 1 which means ${\color{red}\boxed {\color{black} { \sigma_h > \sigma_v}}}$

So the correction option is : $\sigma'_v < \sigma'_h$

Learn more : Gate syllabus for Civil Engineering

Question 19.

With respect to fluid flow, match the following in Column X with Column Y :

Column X Column Y

P . Viscosity 1. Mach number

Q. Gravity 2. Reynolds number

R. Compressibility 3. Euler number

S. Pressure 4. Froude number

Which one of the following combinations is correct?

Column X	Column Y
P . Viscosity	1. Mach number
Q. Gravity	2. Reynolds number
R. Compressibility	3. Euler number
S. Pressure	4. Froude number

P – 2, Q – 4, R – 1, S – 3

P – 3, Q – 4, R – 1, S – 3

P – 4, Q – 2, R – 1, S- 3

P – 2 Q – 4, R – 3, S – 1

Previously Asked in : Gate CE 2022 shift 1 ||

Detailed Explanation

Reynold’s number (R_e) :

Reynold’s number is defined as square root of ratio of inertia force to viscous force in fluid flow.

$\textrm{R}_e = \dfrac{\textrm{inertial force}}{\textrm{ viscous force}} = \dfrac {\rho L^2v^2}{\mu vL}$

${\color{red}\boxed{\color{black}{ \therefore R_e = \dfrac {\rho v L} {\mu} }}}$

it is defined when apart from inertial force, viscous forces are dominant.
Based on this flow can be considered as either laminar or turbulent.
it is a dimensionless quantity

Froude’s number (F_e) :

Froude number is defined as square root of ratio of inertia force to gravitational force.

F_e $= \sqrt{\dfrac{\textrm{Inertial force}} {\textrm{Gravity force}}} = \sqrt {\dfrac{ \rho V^2L^2}{\rho L^3g}}$

${\color{red}\boxed{\color{black}{ \therefore \; \textrm{F}_e = \dfrac{V} {\sqrt{gL}} }}}$

It is used when in addition to inertial forces are important
It governs the fluid flow in open channels
Froude number is dimensionless quantity

Euler number (E_u) :

It is defined as square root of ratio of inertia force to pressure force

$\textrm{E}_u = \sqrt{\dfrac {\textrm{Inertial force}}{\textrm{Pressure force }}} =\sqrt{\dfrac{\rho V^2L^2} {PL^2}}$

${\color{red}\boxed{\color{black}{\therefore \; E_u = \dfrac {V}{\sqrt{\dfrac{P}{\rho}}} }}}$

Euler number is used when apart from inertial force, only pressure forces are dominant
It governs the fluid flow in pipes
It is dimensionless quantity

Mach number (M) :

It is defined as the ratio of flow velocity past a boundary to the local speed of sound.

M = $\sqrt {\dfrac {\textrm{Inertial force}} {\textrm{Elastic force}} }$

= $\sqrt { \dfrac{ \rho L^2 V^2}{K L^2}} = \dfrac {V} {\sqrt{\dfrac{K}{\rho}}} = \dfrac {V} {C}$ where C = velocity of sound in the medium

${\color{red} \boxed{\color{black}{\therefore \; \textrm{M} = \dfrac {V}{C} }}}$

Mach number is used when in addition to inertial force, compressibility forces are dominant.
It is related to compressibility of fluid flow
It is also dimensionless quantity

Correct option is: P – 2, Q – 4, R – 1, S – 3

Question 20.

Let $\psi$ represent soil suction head and K represent hydraulic conductivity of the soil. If the soil moisture content $\theta$ increases, which one of the following statements is TRUE ?

\psi

decreases and K increases.

\psi

increases and k decreases.

Both

\psi

and K decrease.

Both

\psi

and K increase.

Previously Asked in : Gate CE 2022 shift 1 ||

Detailed Explanation

$h_c \propto \dfrac{1}{R}$

$K \propto S$

Water content $\uparrow \to R \uparrow ; R\uparrow \to h_c \downarrow \to \psi \downarrow$

Water content $\uparrow \to S\uparrow \to K \uparrow$

The hydraulic conductivity of the unsaturated soils is the non -linear function of soil suction head ( $\psi$ ) and soil moisture content ( $\theta$ ).
The hydraulic conductivity for coarse textured soil is smaller than for finer textured soil.
On increasing the water content, the soil suction head ( $\psi$ ) decreases, and hydraulic conductivity (K) increases.

Correct option is: $\psi$ decreases and K increases.

Please Help us to make it error free. So if you found any kind of error/mistake, do report us by click here or drop a Mail @ admin@civilenggpro.com

Share on

Print Facebook WhatsApp Telegram

Gate 2022 Civil Engineering solved paper with full explanation forenoon session

Consider the following expression:
$z = sin (y + it) + cos(y - it)$
where $z, y \textrm{ and} \, t$ are variable, and $i = \sqrt {-1}$ is a complex number. The partial differential equation derived from the above expression is

Detailed Explanation

For the equation
$\dfrac {d^3y} {dx^3} + x \left (\dfrac{dy} {dx} \right) ^{ 3/2} + x^2y = 0$
the correct description is

Detailed Explanation

The hoop stress at a point on the surface of a thin cylindrical pressure vessel is computed to be 30.0 MPa. The value of maximum shear stress at this point is

Detailed Explanation

In the context of elastic theory of reinforced concrete, the modular ratio is defined as the ratio of

Detailed Explanation

Which of the following equations is correct for the pozzolanic reaction?

Detailed Explanation

Consider the cross-section of a beam made up of thin uniform elements having thickness t (t << a) shown in the figure above. The (x,y) co-ordinates of the points along the center-line of the cross-section are given in the figure.
The co-ordinates of the shear center of this cross-section are:

Detailed Explanation

Shear center :

Few points should be remembered for finding the location of shear center on any cross section.

Examples :

Four different soils are classified as CH, ML, SP and SW, as per the Unified soil classification system.
Which one of the following options correctly represents their arrangement in the decreasing order of hydraulic conductivity?

Detailed Explanation

Let $\sigma'_v \textrm{and} \sigma'_h$ denote the effective vertical stress and effective horizontal stress, respectively.
Which one of the following conditions must be satisfied for a soil element to reach the failure state under Rankine’s passive earth pressure condition?

Detailed Explanation

Types of earth pressure :

With respect to fluid flow, match the following in Column X with Column Y :

Column X Column Y

P . Viscosity 1. Mach number

Q. Gravity 2. Reynolds number

R. Compressibility 3. Euler number

S. Pressure 4. Froude number

Which one of the following combinations is correct?

Detailed Explanation

Reynold’s number (R_e) :

Froude’s number (F_e) :

Euler number (E_u) :

Mach number (M) :

Let $\psi$ represent soil suction head and K represent hydraulic conductivity of the soil. If the soil moisture content $\theta$ increases, which one of the following statements is TRUE ?

Detailed Explanation

Leave a Comment Cancel reply

Consider the following expression: z = sin (y + it) + cos(y - it) where z, y \textrm{ and} \, t are variable, and i = \sqrt {-1} is a complex number. The partial differential equation derived from the above expression is

Detailed Explanation

For the equation \dfrac {d^3y} {dx^3} + x \left (\dfrac{dy} {dx} \right) ^{ 3/2} + x^2y = 0 the correct description is

Detailed Explanation

The hoop stress at a point on the surface of a thin cylindrical pressure vessel is computed to be 30.0 MPa. The value of maximum shear stress at this point is

Detailed Explanation

In the context of elastic theory of reinforced concrete, the modular ratio is defined as the ratio of

Detailed Explanation

Which of the following equations is correct for the pozzolanic reaction?

Detailed Explanation

Consider the cross-section of a beam made up of thin uniform elements having thickness t (t << a) shown in the figure above. The (x,y) co-ordinates of the points along the center-line of the cross-section are given in the figure.The co-ordinates of the shear center of this cross-section are:

Detailed Explanation

Shear center :

Few points should be remembered for finding the location of shear center on any cross section.

Examples :

Four different soils are classified as CH, ML, SP and SW, as per the Unified soil classification system.Which one of the following options correctly represents their arrangement in the decreasing order of hydraulic conductivity?

Detailed Explanation

Let \sigma'_v \textrm{and} \sigma'_h denote the effective vertical stress and effective horizontal stress, respectively.Which one of the following conditions must be satisfied for a soil element to reach the failure state under Rankine’s passive earth pressure condition?

Detailed Explanation

Types of earth pressure :

With respect to fluid flow, match the following in Column X with Column Y : Column X Column Y P . Viscosity 1. Mach number Q. Gravity 2. Reynolds number R. Compressibility 3. Euler number S. Pressure 4. Froude number Which one of the following combinations is correct?

Detailed Explanation

Reynold’s number (Re) :

Froude’s number (Fe) :

Euler number (Eu) :

Mach number (M) :

Let \psi represent soil suction head and K represent hydraulic conductivity of the soil. If the soil moisture content \theta increases, which one of the following statements is TRUE ?

Detailed Explanation

Leave a Comment Cancel reply

Consider the following expression:
$z = sin (y + it) + cos(y - it)$
where $z, y \textrm{ and} \, t$ are variable, and $i = \sqrt {-1}$ is a complex number. The partial differential equation derived from the above expression is

For the equation
$\dfrac {d^3y} {dx^3} + x \left (\dfrac{dy} {dx} \right) ^{ 3/2} + x^2y = 0$
the correct description is

Consider the cross-section of a beam made up of thin uniform elements having thickness t (t << a) shown in the figure above. The (x,y) co-ordinates of the points along the center-line of the cross-section are given in the figure.
The co-ordinates of the shear center of this cross-section are:

Four different soils are classified as CH, ML, SP and SW, as per the Unified soil classification system.
Which one of the following options correctly represents their arrangement in the decreasing order of hydraulic conductivity?

Let $\sigma'_v \textrm{and} \sigma'_h$ denote the effective vertical stress and effective horizontal stress, respectively.
Which one of the following conditions must be satisfied for a soil element to reach the failure state under Rankine’s passive earth pressure condition?

With respect to fluid flow, match the following in Column X with Column Y :

Column X Column Y

P . Viscosity 1. Mach number

Q. Gravity 2. Reynolds number

R. Compressibility 3. Euler number

S. Pressure 4. Froude number

Which one of the following combinations is correct?

Reynold’s number (R_e) :

Froude’s number (F_e) :

Euler number (E_u) :

Let $\psi$ represent soil suction head and K represent hydraulic conductivity of the soil. If the soil moisture content $\theta$ increases, which one of the following statements is TRUE ?