Below the 10 Questions of aptitude which were asked in gate 2022 Civil Engineering paper- forenoon session.
Let’s start
Question 01.
You should ____ when to say ____.
Previously Asked in : Gate CE-forenoon season 2022 ||
know / known
know / no
no / no
no / know
Answer
Option know / no is correct
Question 02.
Two straight lines pass through the origin (x_0, y_0) = (0,0) . One of them passes through the point (x_1, y_1) = (1,3) and the other passes through the point (x_2, y_2) = (1,2) .
What is the area enclosed between the straight lines in the interval [0,1] on the x-axis?
Previously Asked in : Gate CE-forenoon season 2022 ||
0.5
1.0
1.5
2.0
Answer (Detailed Solution Below)
Option 0.5 is correct
Detailed Explanation :
Equation of first straight line passing through (0,0) and (1,3)
\Rightarrow y - y_1 =\left ( \dfrac {y_2 - y_1} {x_2 - x_1} \right) (x - x_1 )
\Rightarrow y - 0 =\left ( \dfrac {3-0} {1-0} \right) ( x - 0)
y = 3x
Equation of second straight line passing through (0,0) and (1,2)
\Rightarrow y - y_1 = \left( \dfrac {y_2 - y_1} {x_2 - x_1} \right) (x - x_1)
\Rightarrow y - 0 = \left( \dfrac {2 - 0} {1 - 0} \right) (x - 0)
y = 2x
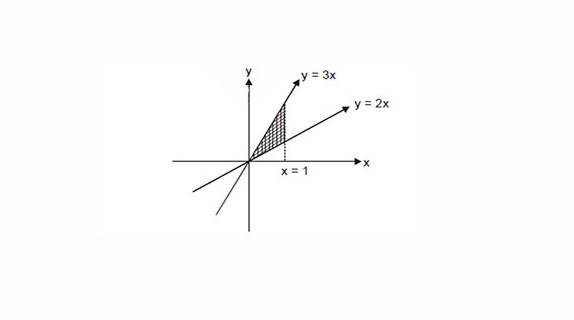
Area = \int_{0}^{1} (3x - 2x) \,dx)
= \bigg( \frac {3x^2} {2} - x^2 \bigg)_{0}^{1}
= \dfrac {1} {2} = 0.5
Another shortcut way is :
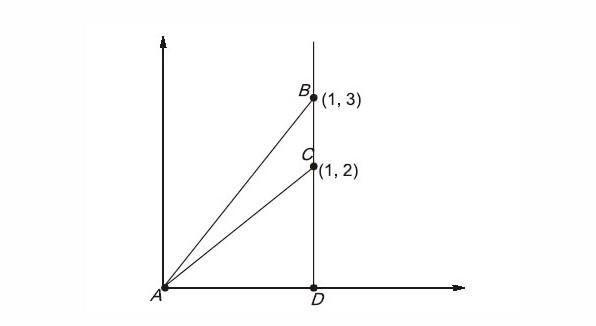
Area ABC, =Area (ABD) – Area (ACD)
= \frac {1}{2} \times 3 \times 1 - \frac {1} {2} \times 2 \times 1 = \frac {1} {2}
= 0.5 {unit}^2
Correct option is 0.5
Question 03.
If \text p : \text q = 1 : 2 ; \text q : \text r = 4 : 3 ; \text r : \text s = 4 : 5 and “u” is 50 \% more than “s “,
what is the ratio of \text p : \text u ?
Previously Asked in : Gate CE-forenoon season 2022 ||
1 : 5
16 : 45
2 : 15
16 : 15
Answer (Detailed Solution Below)
Option 16 : 45 is correct
Detailed Explanation :
Given \dfrac {p} {q} = \dfrac {1} {2}, \dfrac {q} {r} = \dfrac {4} {3}, \dfrac {r} {s} = \dfrac {4} {5}
\Rightarrow \dfrac {r} {s} = \dfrac {4 \times 3} {5 \times 3}
\Rightarrow \dfrac {q} {r} = \dfrac {4 \times 4} {3 \times 4}
\Rightarrow \dfrac {p} {q} = \dfrac {1 \times 8} {2 \times 8 }
From above p : q : r : s \\8 : 16 : 12 : 15
\therefore \, s = 15\\ \textrm{so} \, u = 15 \times 15 = 22.5
now \dfrac {p} {q} = \dfrac {8} {22.5}
= \dfrac {80} {225} = \dfrac {16} {45}
Correct option is : 16 : 45
Question 04.
Given the statements :
- P is the sister of Q
- Q is the husband of R
- R is the mother of S
- T is the husband of P
Based on the above information, T is ______ of S.
Previously Asked in : Gate CE-forenoon season 2022 ||
the grandfather
an uncle
the father
a brother
Answer (Detailed Solution Below)
Option an uncle is correct
Detailed Explanation :
T is the husband of P
P is the sister of Q
Q is the husband of R
R is the mother of S
From the above statements, it is clear T is an uncle-in-law of S
Correct option is: an uncle
Question 05.
In the following diagram, the point R is the center of the circle. The lines PQ and ZV are tangential to the circle. The relation among the areas of the squares, PXWR, RUVZ and SPQT is
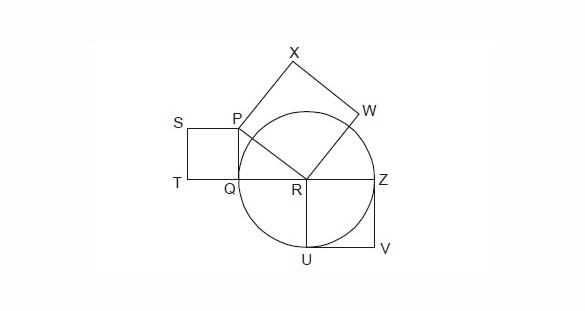
Previously Asked in : Gate CE-forenoon season 2022 ||
Area of PXWR = Area of RUVZ – Area of SPQT
Area of PXWR = Area of SPQT – Area of RUVZ
Area of SPQT = Area of PXWR – Area of RUVZ
Area of SPQT = Area of RUVZ = Area of PXWR
Answer (Detailed Solution Below)
Option Area of SPQT = Area of PXWR – Area of RUVZ is correct
Detailed Explanation
From \triangledown \; PQR by Pythagoras theorem,
\Rightarrow {PR}^2 = {PQ}^2 + {QR}^2
Also, QR = RZ ,
\Rightarrow {PR}^2 = {PQ}^2 + {RZ}^2
\Rightarrow \text {Area \, of \,} PXWR = \text {Area \,of \,} SPQT +\text{ Area \,of \,} RUVZ
\Rightarrow \text {Area \, of \,} SPQT = \text {Area \, of \, } PXWR \,- \,\text {Area\, of\,} RUVZ
Correct option is : Area of SPQT = Area of PXWR – Area of RUVZ
Learn more : Previous year Gate papers of Civil Engineering with detailed solution
Learn more : GATE 2022 All branches Aptitude Questions with detailed Solution
Question 06.
Healthy eating is a critical component of healthy aging. When should one start eating healthy? It turns out that it is never too early. For example, babies who start eating healthy in the first year are more likely to have better overall health as they get older.
Which one of the following is the CORRECT logical inference based on the information in the above passage?
Previously Asked in : Gate CE-forenoon season 2022 ||
Healthy eating is important for those with good health conditions, but not for others
Eating healthy can be started at any age, earlier the better
Eating healthy and better overall health are more correlated at a young age, but not older age
Healthy eating is more important for adults than kids
Answer
Option Eating healthy can be started at any age, earlier the better is correct
Question 07.
P invested Rs 5000 per month for 6 months of a year and Q invested Rs X per month for 8 months of the year in a partnership business. The profit is shared in proportion to the total investment made in that year.
If at the end of that investment year, Q receives \frac {4} {9} of the total profit, what is the value of (in Rs )?
Previously Asked in : Gate CE-forenoon season 2022 ||
2500
3000
4687
8437
Answer (Detailed Solution Below)
Option 3000 is correct
Detailed Explanation :
Let total profit = y
So, profit by Q = \dfrac {4} {9} y
Profit by P = y - \dfrac {4} {9}y = \dfrac {5y} {9}
\dfrac {\text {Profit \, by} \, P} {\text{ Profit \, by }\,Q} = \dfrac {5} {9}
\dfrac {5} {4} = \dfrac {C_p T_p} {C_q T_q}
\dfrac {5}{4} = \dfrac {5000 \, \times 6} {X \times 8}
X= \dfrac {5000 \times 6 \times 4} {8 \times 5}
X = 3000
Correct option is : 3000
Question 08.
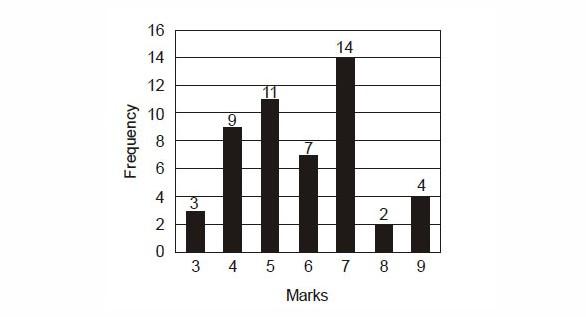
The above frequency chart shows the frequency distribution of marks obtained by a set of students in an exam.
From the data presented above, which one of the following is CORRECT?
Previously Asked in : Gate CE-forenoon season 2022 ||
mode > median > mean
mean > mode > median
mode > mean > median
median > mode > mean
Answer (Detailed Solution Below)
Option mode > median > mean is correct
Detailed Explanation :
Mean = \dfrac {f_1 x_1 \; + \; f_2 x_2 \,...... \,+ \; f_7 x_7 } { f_1 \;+\; f_2 + \;f_3 ..... \;+ \;f_7}
= \frac {3 \times 3 + 9 \times 4 + 11 \times 5 + 7 \times 6 + 14 \times 7 + 2 \times 8 + 4 \times 9} {3 + 9 + 11 + 7 + 14 + 2 + 4}
= \dfrac {292} {50} = 5.84
Median = \dfrac{ \left(\frac{n} {2}\right)^ {th} \; + \; \left (\frac {n} {2} \;+ \;1\right)^{th}} {2}
= \dfrac { \left(\frac {50}{2}\right)^{th} + \left ( \frac {50} {2} + 1\right) ^ {th}} {2}
= \dfrac {(25)^ {th} + (26)^{th}} {2}
= \dfrac {6 + 6} {2}
= 6
Mode = observation (data with high frequency)
= 7
Hence correct option is : Mode > Medium > Mean
Learn more : Gate syllabus for Civil Engineering
Question 09.
In the square grid shown below, a person standing at P_2 position is required to move to P_5 position.
The only movement allowed for a step involves, “two moves along one direction followed by one move in a perpendicular direction”. The permissible directions for movement are shown as dotted arrows in the right. For example, a person at given position Y can move only to the positions marked X on the right.
Without occupying any of the shaded squares at the end of each step, the minimum number of steps required to go from P_2 to P_5 is
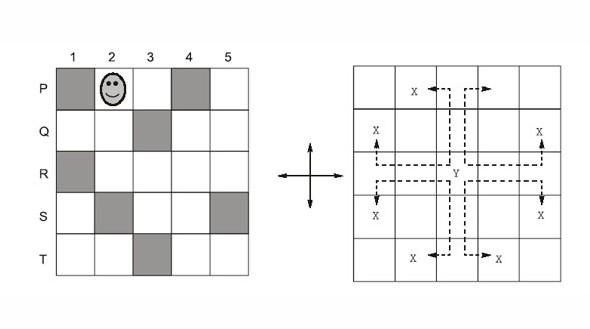
Previously Asked in : Gate CE-forenoon season 2022 ||
5
4
6
7
Answer
Option 5 is correct
Question 10.
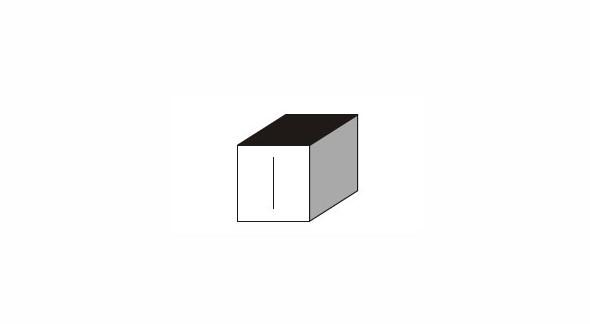
Consider a cube made by folding a single sheet of paper of appropriate shape. The interior of the cube are all blank. However, the exterior faces that are not visible in the above view may not be blank.
Which one of the following represents a possible unfolding of the cube?
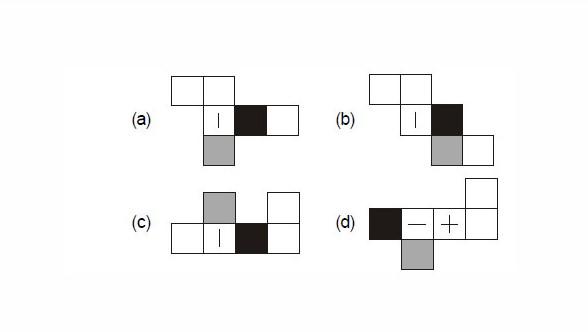
Previously Asked in : Gate CE-forenoon season 2022 ||
a
c
b
d
Answer
Option d is correct
Black edge is perpendicular to given line and white shaded edge is parallel to given line so only possibility of d
Quick links :
Please Help us to make it error free. So if you found any kind of error/mistake, do report us by click here or drop a Mail @ admin@civilenggpro.com
